| Les Instal·lacions: |
| Trobaràs les característiques tècniques de les nostres instal·lacions. |
| |
| Els Trens: |
| Un recull de tot el material construït per els socis del Tren de Palau. |
| |
| Els Horaris : |
| Si vols venir amb nosaltres aquí tens els nostres horaris. |
| |
| La Nit del Tren : |
| Al solstici d'estiu es la festa principal de la Associació. |
| |
| Galeria de videos : |
| També nosaltres hem gravat vídeos, estan posats a Youtube, però aquí tens la col•lecció per no anar-los buscant. |
| |
| Imatges de trens : |
| Imatges en que sumen els paisatges del Parc de l'Hostal de Fum amb el Tren de Palau. |
| |
| Imatges del inici : |
| Fotografies que per nosaltres ja son història. |
| |
| Imatges de la nevada : |
| Nevada del 28 de febrer de 2018 amb fotografies d'en Jordi Valero i Ricard Soler |
| |
| Extensió Via 4: |
| Es un butlletí que entreguem regularment a tots els socis i altres associacions. |
| |
| El Poble : |
| Habitat des de la prehistòria, aquest indret apareix en documents de fa mil anys. |
| |
| Llocs d'interès : |
| Al poble de Palau-solità i Plegamans podem trobar tot un munt de llocs que poden ser del nostre interès i que podem visitar. |
| |
| Els Enllaços : |
| No som els únics en el mon dels trens. Aquí tens alguns enllaços amb companys de la nostra afició. |
| |
| Els Documents : |
| Un petit arxiu del Tren de Palau per consultar. |
| |
| El Calderí |
| Era el "tren de Caldes", o sigui de Mollet a Caldes de Montbui, per Palau. Per això el nostre es diu "Tren de Palau", en record del seu germà gran, tants anys absent. |
| |
| Els Trens Petits |
| Una intensa i llarga historia dels petits trens artesanals, recreatius i tripulats. Els primers anys del Tren de Palau. |
| |
| FIVV |
| Fotografies recuperades de l'oblit i després de la seva acurada restauració, són comentades per un expert en història ferroviària que les fan doblement atractives. |
| |
| Edmondson: |
| Historia dels clàssics bitllets de molts ferrocarrils. |
| |
| Els Ponts: |
| Els ponts de gelosia, una petita descripció d'aquestes fascinats estructures. |
| |
|
 |
|
 |
| Coeficient de dilatació |
El coeficient de dilatació lineal és l'augment o disminució de la longitud d'una barnilla de 1 metro de longitud, quan augmenta o disminueix 1ºC la seva temperatura normal.
En el ferro es de 12 mil·lèsimes de mil·límetre, i en altres metalls...
Les vies del Tren de Palau es formen amb barres llargues de 12 metres de longitud, obtingudes unint, soldats a testa, 2 perfils laminats "U" de 40 mm, de 6 metres cada un.
En aquestes barres de ferro exposades a l'aire lliure (sol i serena), la diferencia de temperatura estiu / hivern pot ser de 50ºC, variant la seva longitud en 7,2 mm. |
 |
| Coeficients de dilatació lineal |
| Ferro |
0,000012 |
| Coure |
0,000018 |
| Llautó |
0,000020 |
| Alumini |
0,000026 |
| Plom |
0,000029 |
|
|
| |
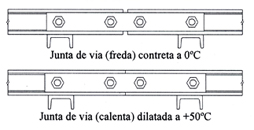
| Les juntes de via, que collades amb cargols uneixen els carrils, ben ajustades mantenen la continuïtat en l'alineació vertical i transversal dels trossos de via, a l'hora que permeten un petit desplaçament longitudinal per a la dilatació. Això últim s'aconsegueix be augmentant el diàmetre del forat per als cargols, o fent aquests forats en trau polís.
Quan, per l'augment de la temperatura o la longitud dels trossos de via, la dilatació demana mes espai que el permès per la folgança dels cargols a les brides, el tros de via quedarà atrapat topant a testa en els extrems, deformant-se serpentejant, elevant-se o augmentant el radi de les corbes. En aquests casos hi ha dos solucions; augmentar el nombre de juntes, o modificar-ne algunes per a que permetin una dilatació mes gran. |
 |
 |
|
| |
| Problema:
Quin serà l'esforç d'empenta "F" que fa un carril de via, quan la seva temperatura, que era de 25ºC el bonic matí de primavera en que el van instal·lar, ha pujat fins a 50ºC un migdia del mes d'agost, o ha baixat fins a 0 graus una nit d'hivern.
Primer cal saber l'àrea de la figura del carril tallat per la secció transversal. Això pot ser complicat de calcular amb la geometria, degut a que hi ha molts arcs i cotes difícils de mesurar amb precisió, però si sabem el pes per metro i la densitat del ferro és molt fàcil.
El carril de via, com sabem, es un perfil de ferro laminat "U de 40" que pesa 2,7 kg per metro, que son 0,027 kg/cm. |
 |
 |
|
Com que la densitat del ferro es 7,8 kg/dm3 (0,0078 kg/cm3), l'àrea s de la figura d'un tall transversal de la barra del carril es de:
s = 0,027 / 0,0078 = 3,46 cm
Ja tenim totes les dades necessàries per aplicar una fórmula que ens ha de donar l'esforç que volem saber:
F = k * E * s * t
En la que :
F= esforç en kg
k= coeficient de dilatació = 0,000012
E= mòdul d'elasticitat = 2000000
s= superfície de la secció = 3,46 cm2
t= variació de temperatura (50> 25> 0)ºC
I aplicant la fórmula tenim que:
F = 0,000012 x 2000000 x 3,46 x 25 ≈ 2 Tm
O sigui, aproximadament dos mil quilos. Aquest es l'esforç que pot arribar a fer, sobre les juntes o els objectes que n'impedeixin la seva dilatació o contracció lineal amb uns variació en mes o en menys 25ºC.
Si no hi ha joc a la junta de la via, i el muntatge s'ha fet a la temperatura mitjana, serà un esforç de dos tones de compressió a l'estiu, i dos tones de compressió a l'estiu, i dos tones de tracció a d'hivern.
Una part d'aquest esforç s'aplica arrossegant-se la via sobre el balast quan es dilata o es contrau, i l'altra part en el fregament que hi ha entre les brides i els carrils a les juntes de via, lliscament per l'espai de joc que s'ha deixat expressament per a la dilatació. |
 |
| Fregament per rodolament |
En el rodolament s’ha de considerar que les dues superfícies només estan en contacte en un punt.
En teoria, el punt no té dimensió. És només un lloc geomètric.
Tots sabem que les potes d’una taula, si acabessin en una punta molt petita i prou dura, ratllarien el terra. El pes es concentraria en una superfície minúscula, i la pressió seria enorme.
La pressió P es la força F dividida per la superfície S.
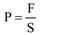
Si la superfície S és un punt no hi ha superfície, és zero. Llavors la pressió seria :
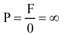
En la pràctica el punt, encara que molt petit, existeix. I a vegades no es tant petit.
En el rodolament, la roda (i tot el pes que hi ha al damunt) es concentra en el punt de contacte roda-carril, i com podem suposar aquest punt, encara que no el veiem, es prou gran com per que la via (en condicions estàtiques) no quedi marcada.
Però la pressió és prou gran per a que, quan una roda circula bloquejada, ràpidament es desgasta produint-se els temuts “plans de rodolament” (planos de rodadura). |
Per tant, en el rodolament no hi ha d’haver mai lliscament. El punt de contacte ha d’anar canviant contínuament donant voltes. El fregament per rodolament serà únicament el que existeixi per la pressió en el punt de contacte.
Quant mes petit sigui el punt de contacte, menor serà el fregament, i al contrari; com mes gran, mes fregament. |
 |
 |
|
Per això, materials tous que es deformen com la goma, donen un coeficient superior al que donen els materials mes durs, com l’acer.
A la pràctica, el coeficient de fregament per rodolament és unes 70 vegades mes petit que el de lliscament.
Això vol dir simplement que, arrossegar un tren amb les rodes voltant normalment, costa (en condicions dinàmiques, o sigui quan ja s’ha iniciat el moviment) un esforç unes 70 vegades menys que fer-ho amb les rodes bloquejades.
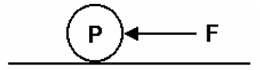
Si volem trobar el valor del coeficient de rodolament, buscarem l’angle d’inclinació de la via en el moment que comença a rodolar lliurement.
Si anem augmentant la força F (aplicada a l’eix de la roda P) fins que comenci a voltar, tindrem el coeficient k de rodolament:
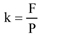
Si ho fem amb una roda de tren sobre una via, comprovarem que, per a mantenir el moviment en via recta horitzontal, només cal fer uns 3 kg de força F per cada Tm de P. O sigui que el coeficient haurà resultat ser de 0’003 (tres mil·lèsimes).
I aquest és el gran avantatge dels ferrocarrils; es transporten grans càrregues amb un esforç comparativament discret. Economia energètica i medi ambiental. |
 |
| Angle de fregament |
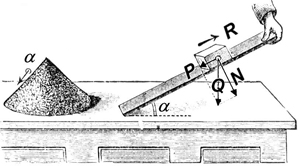
| Un objecte, per exemple un tros de guix, pot quedar-se quiet sobre una fusta inclinada, però si l'anem inclinant cada vegada una mica mes, en arribar a un determinat angle a, el tros de guix comença a lliscar cap avall.
L'angle α es coneix com angle de fregament. Del seu valor es dedueix el coeficient de fregament f entre el guix i la fusta.
f = tg α
Tots hem vist com en descarregar un camió de sorra es fa una pila de forma cònica. |
 |
 |
|
| Però cal saber que la conicitat mes o menys pronunciada depèn del tipus de material. No fa el mateix angle una pila de sorra fina, que una pila de grabeta o de farina.
Proveu de fer una pila amb boles de coixinet.
Qüestió: Perquè no es pot aconseguir que el pendent a d'una pila cònica de sorra excedeixi d'un determinat límit?
Resposta: Perquè el pendent màxim tindrà un valor que dependrà del coeficient de fregament de la sorra amb la pròpia sorra. Amb aquesta qüestió està relacionat l'angle que s'ha de donar als talussos per a evitar el corriment de terres, que ha de ser diferent en determinats terrenys d'acord amb la seva diferent naturalesa. |
 |
| El límit d'elasticitat |
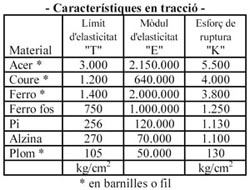
| El límit d'elasticitat "T" es l'esforç màxim que pot resistir un material, conservant la propietat de poder recuperar, per si mateix la forma inicial, quan se l'allibera d'aquest esforç.
Si s'augmenta l'esforç superant el límit d'elasticitat "T", primer es produeix un allargament o deformació permanent que ja no es recupera quan cessa l'esforç, i si es segueix augmentant l'esforç, s'arriba al punt de ruptura "K" en que es trenca el material.
Un coeficient de seguretat s'ha d'aplicar sempre, reduint l'esforç màxim de treball previst per sota de "T". Per als metalls acostuma a ser de 1/6, i per a les fustes 1/10. El coeficient de seguretat pot ser mes gran, en funció de cada cas. |
 |
| El coeficient d'allargament |
| El coeficient d'allargament "α", és el petit allargament que experimenta una mostra de material, formada per una barnilla de 1 metro de longitud i 1 cm2 de secció, quan està sotmesa a l'esforç de tracció d'1 kg.
Com que "α" pot resultar un número molt petit, per a facilitar els càlculs, s'utilitza el concepte mòdul d'elasticitat "E", que es la seva inversa, o sigui : E = 1/α.
"Tratado Popular de Física" J.Kleiber/Dr.B.Karsten
Editorial Gustavo Gili - MCMXIX - Barcelona |
|
 |
|
 |
| Prova dinamomètrica |
| Dissabte 14 de juliol s'ha realitzat una prova dinamomètrica per a saber quin es l'esforç als ganxos que proporciona el material motor, donant els resultats següents: |
| Màquina |
kg |
| AA-A-2101 |
130 |
| BB-4221-9 |
140 |
| BB-1601 |
120 |
| A1 |
130 |
| D9 |
130 |
| L801 |
120 |
|
Cal destacar que va ser una prova estàtica, amb la màquina immòbil, només tibant però sense avançar, o sigui a velocitat zero.
Tots sabem que la potencia és l'esforç multiplicat per la velocitat, o el que es el mateix, el treball dividit pel temps. Per tant, com que no hi havia moviment, l'espai era sempre zero, i la potencia en tots els casos també igual a zero. |
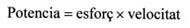
|
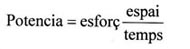 |
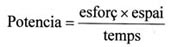 |
El que es mesurava era únicament l'esforç.
La constància de l'esforç a diferents velocitats es una característica pròpia de cada màquina o sistema de motorització.
Alguns poden mantenir l'esforç constant dintre d'una gamma de velocitats (el mateix esforç a qualsevol velocitat), i altres poden mantenir la potència constant (l'esforç es redueix a mesura que augmenta la velocitat). |
 |
| puja --->> |
| 08-10-2013 |
|